Physics goals - The Double Beta Decay

Home

Conferences

Collaboration

Publications

SuperNEMO

Private

The two neutrino double beta decay

In 1935, Maria Goeppert-Mayer predicted the existence of the two neutrino double beta decay process (DBD).

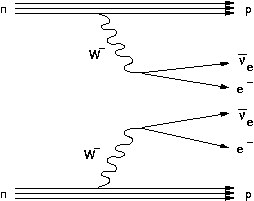
This decay mode is theoretically allowed in the SM framework; it is labelled ββ2ν. This process (the β^-β^- mode) consists in the simultaneous transmutation of two neutrons into protons inside a nucleus thanks to β decay like processes (figure 10).

Note: β⁺β⁺ decay exists too...

Figure 10: Double beta decay; two neutrons are changed into protons inside the nucleus, emitting two electrons and two antineutrinos.

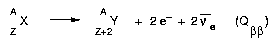
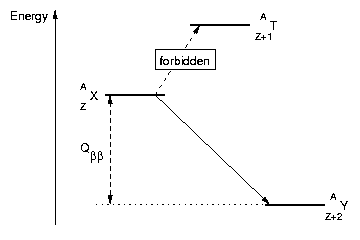
The double beta decay process can be observed in a few isotopes for which all other decay channels are forbidden for energetic reasons (figure 11).

Figure 11: Energy scheme for the double β^- decay from parent nucleus ^AX to daughter nucleus ^AY. The single β^- decay to the intermediate isotope ^AT is forbidden by the energy conservation rule.

Calculations predict that this process is very rare, with mean lifetimes of the order of 10^18-24 years depending of the emitter isotope. The half life time is given by the following formula:

Where:
• a_2ν ~ 2 10^-22 y^-1 is a dimensional factor
  
• F_2ν is a known phase space factor proportionnal to Q_ββ¹¹
  
• M_2ν is the nuclear matrix element (n.m.e.).

Only a few ββ emitting isotopes are good candidates for experimental studies. They are shown in table 4. The ββ2ν process have been experimentally observed for most of them.

Suppose we use 1 kg of ¹⁰⁰Mo (10 moles), how many ββ2ν decays do we get in one year?
Answer:

where N_A is the Avogadro constant.

Assuming that our ¹⁰⁰Mo sample is contaminated by some natural ²¹⁴Bi radioactivity at the level of 1 Bq/kg, we get about 3 10⁷ beta decays due to natural ²¹⁴Bi radioactivity for the same period: this is about two orders of magnitude higher than the expected number of ββ2ν events. That means that natural radioactivity is likely to act as a background provider, preventing an efficient direct observation of the very rare double beta process.

The neutrinoless double beta decay

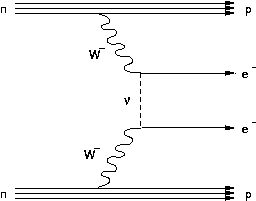
In 1939, Wolfgang Furry proposed that a double beta decay without emission of neutrino (labelled ββ0ν) could occur in ββ emitting nuclei if new physics exist beyond the standard model. In ββ0ν decay, two neutrons in a nucleus are simultaneously changed in protons emitting two electrons but without emitting any anti-neutrinos (figure 12).

Figure 12: The ββ0&nu decay; only two electrons are emitted while two neutrons simultaneously transmute into two protons.

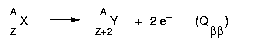
The existence of such a process violates the lepton number conservation rule, thus it is forbidden by the SM. Nevertheless, ββ0ν decay could exist if (figure 13):

• (anti-)neutrinos have a non zero mass,
• neutrinos are a Majorana particles, i.e. neutrinos and anti-neutrinos are the same particle.

Figure 13: Feynman diagram for the neutrinoless double beta decay (ββ0&nu). This process could be observed thanks to the exchange of a Majorana massive neutrino between the two W^- bosons.

Note: other mechanisms have also been invented to explain such a process.

Neutrinoless double beta decay is the only known process that enables to test experimentally the Majorana nature of neutrino together with its absolute mass scale. That makes this topics very attractive.

The half life time is given by the following formula:

Where:
• a_0ν ~ 5 10^-17 y^-1 is a dimensional factor
  
• F_0ν is a known phase space factor proportionnal to Q_ββ⁵
  
• M_0ν is the nuclear matrix element (n.m.e.).
• η = <m_ν>/m_e with <m_ν> being the effective mass of the exchanged neutrino and m_e the mass of the electron (0.511 MeV/c²).

From the formula above, we see that the observation of the ββ0ν process enables the estimation of the (Majorana) neutrino mass scale <m_ν>. Here again the calculation of the nuclear matrix element is an important source of uncertainty.